Definition and formula of the amount of heat
The internal energy of a thermodynamic system can be changed in two ways:
- doing work on the system,
- using thermal interaction.
The transfer of heat to a body is not associated with the performance of macroscopic work on the body. In this case, the change in internal energy is caused by the fact that individual molecules of a body with a higher temperature do work on some molecules of a body that has a lower temperature. In this case, thermal interaction is realized due to thermal conductivity. Energy transfer is also possible using radiation. The system of microscopic processes (relating not to the whole body, but to individual molecules) is called heat transfer. The amount of energy that is transferred from one body to another as a result of heat transfer is determined by the amount of heat that is transferred from one body to another.
Definition
Warmth
is the energy that is received (or given up) by a body in the process of heat exchange with surrounding bodies (environment). The symbol for heat is usually the letter Q.
This is one of the basic quantities in thermodynamics. Heat is included in the mathematical expressions of the first and second laws of thermodynamics. Heat is said to be energy in the form of molecular motion.
Heat can be transferred to the system (body), or it can be taken from it. It is believed that if heat is transferred to the system, then it is positive.
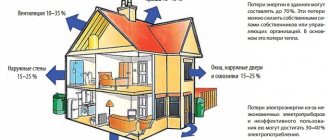
Heat gains from people
The amount of heat generated by people in a room is always positive. It depends on the number of people in the room, the work they perform and air parameters (temperature and humidity).
In addition to tangible (sensible) heat, which the human body transfers to the environment through convection and radiant energy, latent heat is also released. It is spent on the evaporation of moisture by the surface of the human skin and lungs.
The ratio of sensible and latent heat released depends on the type of person’s occupation and air parameters. The more intense the physical activity and the higher the air temperature, the greater the proportion of latent heat; at an air temperature above 37 degrees, all the heat generated by the body is released through evaporation.
- For any type of activity - from sleep to heavy work - heat generation is greater at low ambient temperatures.
- The higher the air temperature, the greater the latent heat generation and the less sensible heat generation.
When calculating the heat emission from people, you need to take into account that the maximum number of people will not always be in the room. The average number of people who will typically be in the room is determined by experience (for example, the number of people in a store), or by using established coefficients (for example, in institutions - 0.95 of the total number of employees).
Table of heat emission from people depending on the ambient temperature and physical activity
| Ambient temperature | Heat dissipation at rest, W | Heat dissipation at light load, W | Heat dissipation under heavy load, W |
| 10 | 130 | 156 | 290 |
| 14 | 118 | 138 | 263 |
| 18 | 104 | 133 | 250 |
| 22 | 102 | 132 | 249 |
| 26 | 102 | 132 | 249 |
| 30 | 100 | 130 | 246 |
| 32 | 98 | 128 | 244 |
Note: the average data is for adult men. It is believed that women produce 85%, and children - 75% of the heat and moisture released by men.
Formula for calculating heat when temperature changes
Let us denote the elementary amount of heat as $\delta Q$. Let us note that the element of heat that the system receives (gives) with a small change in its state is not a complete differential. The reason for this is that heat is a function of the process of changing the state of the system.
The elementary amount of heat that is imparted to the system, and the temperature changes from T to T+dT, is equal to:
$$\delta Q=C d T(1)$$
where C is the heat capacity of the body. If the body in question is homogeneous, then formula (1) for the amount of heat can be represented as:
$$\delta Q=cmd T=\nu c_{\mu} d T(2)$$
where $c=\frac{C}{m}$ is the specific heat capacity of the body, m is the mass of the body, $c_{\mu}=c \cdot \mu$ is the molar heat capacity, $\mu$ is the molar mass of the substance, $ \nu=\frac{m}{\mu}$ is the number of moles of the substance.
If the body is homogeneous and the heat capacity is considered independent of temperature, then the amount of heat ($\Delta Q$) that the body receives when its temperature increases by $\Delta t = t_2 - t_1$ can be calculated as:
$$\Delta Q=cm \Delta t(3)$$
where t2, t1 body temperature before and after heating. Please note that when finding the difference ($\Delta t$) in the calculations, temperatures can be substituted both in degrees Celsius and in kelvins.
A little history
Numerous experiments carried out at the end of the 18th and beginning of the 19th centuries made it possible not only to establish the basic properties and laws of electricity, but also to formulate an epoch-making conclusion about the equivalence between heat and mechanical work: work, or, as they later began to formulate, “energy” , is never lost, but only passes from one type to another. This conclusion, which later received the name of the law of conservation and transformation of energy (see subsection 1.2), was that heat can be converted into mechanical work and vice versa, and that from a certain amount of heat only a certain amount of mechanical work can be obtained. One can cite thousands of examples where, with the help of this law, the results of experiments in various fields of natural science were objectively interpreted.
Joule Lenz's law in brief
Electrical engineers also used the basic principles of the law of conservation of energy to determine, for example, the amount of thermal energy released in a galvanic battery as a result of a chemical reaction and subsequently converted into electrical energy. However, the peculiarity of electrical energy is that electricity itself is not applicable. Humanity cannot use it directly, just as it is warmed by heat, sees through light, etc. You can only use the action of electric current, in which electricity is converted into other forms of energy.
One of the first to deeply study the properties of electric current in 1801–1802 was St. Petersburg academician V.V. Petrov (1761–1834), who conducted many experiments to study the laws of electric current unknown at that time. Having studied the work of his predecessors, Petrov came to the conclusion that a more complete and comprehensive study of electric current is possible only with the help of large galvanic batteries, the action of which will be more intense and easier to observe. For his experiments, Petrov built the largest battery in the world in those years, consisting of 4,200 copper and zinc circles placed in four wooden boxes, and received from it an electromotive force of about 1,700 volts. Thanks to the “lying” design, the heavy metal mugs did not squeeze out the liquid that soaked the paper mugs that separated the zinc and copper elements. To insulate, he coated the inside walls of the drawers with wax varnish. The total length of the battery was 12 m. All this allowed him to build a “huge, especially” battery, which the world had not yet known. Already in 1801, he found the dependence of the current on the cross-section of the conductor, while the German physicist Ohm, who worked on these problems, published the results of his experiments only in 1827. Very soon he noticed that when an electric current passes through a conductor, the latter heats up.
In his works V.V. Petrov describes experiments on the electrolysis of vegetable oils, as a result of which he discovered the high electrical insulating properties of these oils. Later, oils were widely used as electrical insulating materials. Wanting to demonstrate the phenomenon of electrolysis simultaneously in several tubes with water, Petrov was the first to use a parallel connection of electric current receivers. The work of this outstanding scientist established the possibility of practical use of electric current to heat conductors.
Emilius Christianovich Lenz (1804–1865) - a famous Russian physicist and electrical engineer, academician of the St. Petersburg Academy of Sciences, rector of St. Petersburg University - was born in Dorpat (now Tartu, Estonia) in the family of an official. After his second year at the University of Dorpat, he set off in 1823 on a three-year voyage around the world. Using the instruments he designed (a depth meter and a bathometer), he carried out physical research in the waters of the Bering Strait, the Pacific and Indian Oceans, established the origin of warm and cold sea currents, and discovered the law of oceanic circulation. In 1829, he took part in an expedition to the Caucasus, where he carried out magnetic, thermometric and barometric measurements in the mountainous regions of the Caucasus and on the coast of the Caspian Sea. In 1830 he was appointed extraordinary professor and director of the physics office at the St. Petersburg Academy of Sciences, in 1836 he headed the department of physics at St. Petersburg University, and in 1863 he became the rector of this university. His main works are devoted to electromagnetism, questions of the theory and practical application of electricity, research in the field of which Lenz began in 1831 in the laboratory of the first Russian electrical engineer - Academician V.V. Petrova. Lenz stood at the origins of the first school of physicists and electrical engineers in Russia, whose followers were A.S. Popov, F.F. Petrushevsky, V.F. Mitkevich et al.
The dependence of the amount of heat released on the current strength was studied by the English physicist James Joule and the Russian physicist Emilius Lenz. They passed current through a spiral placed in a calorimeter with water. After some time the water warmed up. From its temperature it was easy to calculate the amount of heat released. From experiments carried out almost simultaneously, Joule and Lenz came to the conclusion that when galvanic current I passes through a conductor with a certain resistance R, work A is performed during time t:
It will be interesting➡ All about Ohm’s law: in simple words with examples for dummies
A = I 2 Rt,
manifested in the form of released heat.
This important conclusion of the reversibility of electrical and thermal energy, theoretically substantiated by William Thomson, was called the Joule-Lenz law, and the unit of mechanical work in the SI system was named after Joule.
By combining conductors of different resistances connected in series in a common circuit, it is possible to achieve the concentrated release of a large amount of heat in a small section of a conductor with a high resistance. All initial experiments in converting the energy of electric current into thermal and even light energy were based on this concentration of heat release.
The essence of this law
All his life V.V. Petrov, a member of two academies, lived modestly and unnoticed. He worked for 41 years at the Medical-Surgical Academy. During this time, he conducted many physical experiments, wrote three books and a textbook on physics, which was used in gymnasiums throughout Russia. Petrov wrote books and scientific articles in Russian so that as many people as possible could read them, although at that time it was customary to write scientific works in Latin. He wrote: “I hope that enlightened and impartial physicists will at least one day agree to give my works the justice that the importance of these latest experiments deserves.”
Formula for the amount of heat during phase transitions
The transition from one phase of a substance to another is accompanied by the absorption or release of a certain amount of heat, which is called the heat of phase transition.
Thus, to transfer an element of matter from the state of a solid to a liquid, it should be given an amount of heat ($\delta Q$) equal to:
$$\delta Q=\lambda dm$$
where $\lambda$ is the specific heat of fusion, dm is the element of body mass. It should be taken into account that the body must have a temperature equal to the melting point of the substance in question. During crystallization, heat is released equal to (4).
The amount of heat (heat of evaporation) required to convert liquid into vapor can be found as:
$$\delta Q=rdm$$
where r is the specific heat of evaporation. When steam condenses, heat is released. The heat of evaporation is equal to the heat of condensation of equal masses of substance.
What is specific heat capacity
Each substance in nature has its own properties, and heating each individual substance requires a different amount of energy, i.e. amount of heat.
The specific heat capacity of a substance is a value equal to the amount of heat that must be transferred to a body with a mass of 1 kilogram in order to heat it to a temperature of 1 0C
Specific heat capacity is designated by the letter c and has a measurement value of J/kg*
For example, the specific heat capacity of water is 4200 J/kg*0C. That is, this is the amount of heat that needs to be transferred to 1 kg of water to heat it by 1 0C
It should be remembered that the specific heat capacity of substances in different states of aggregation is different. That is, heating ice by 1 0C will require a different amount of heat.